Table of Contents
Introduction
Have you ever looked at a sunflower, a seashell, or a pinecone and wondered why it looks so perfectly shaped? It almost feels like nature is following a secret plan. Imagine nature as a quiet artist, counting numbers as it paints leaves, flowers, and spirals all around us.
This quiet counting follows a simple number pattern called the Fibonacci sequence. It starts with two easy numbers: 0 and 1. After that, each new number is made by adding the two before it—1, 2, 3, 5, 8, 13, and more.
Even though it is just a list of numbers, this pattern appears all over nature. You can see it in how leaves grow on a stem, how many petals a flower has, and how shells and even galaxies form beautiful spirals.
Nature uses the Fibonacci sequence because it helps things grow in the smartest way. Plants get more sunlight, flowers have room to spread seeds, and shells grow strong without wasting energy. These Fibonacci patterns show us how nature stays balanced and uses space wisely.
What is the Fibonacci Sequence?

The Fibonacci sequence is a series of integers known as Fibonacci numbers. It typically starts with 0 and 1, followed by another 1, and continues with each number being the sum of the two before it.
In this sequence, each term is formed by adding the two previous terms together. The first 14 numbers in the sequence are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and 233. For example, the third number (1) is the result of adding the first two (0 and 1), and this pattern continues for every number that follows.
This sequence can go on infinitely by applying the same rule. While some variations of the sequence begin with 1 instead of 0, starting with 0 is the more widely accepted convention.
Beauty of the Fibonacci Pattern in Nature
The Fibonacci pattern in nature is more than just a mathematical curiosity—it’s a fundamental blueprint seen across the natural world.
- From the spiral of galaxies to the arrangement of sunflower seeds, Fibonacci numbers in nature help explain how life optimizes growth, balance, and symmetry.
- One of the most breathtaking examples is the Fibonacci spiral in nature—visible in the curling of fern fronds, pinecones, and even hurricanes.
- These spirals are not random; they follow a precise numerical order derived from the Fibonacci sequence and nature’s design.
- Each number in the sequence is the sum of the two preceding ones, and this progression manifests in the way petals, leaves, and shells arrange themselves to maximize exposure to sunlight and space.
Scientists and naturalists alike are fascinated by the recurring presence of Fibonacci patterns in nature, considering them a bridge between mathematics and biology.
- Whether you’re observing a nautilus shell, a sunflower head, or a Romanesque broccoli, the same underlying ratios appear—revealing a profound connection between numbers and the world we live in.
- The Fibonacci number in nature isn’t just theoretical—it’s practical, efficient, and astonishingly beautiful. It shows us how nature, through millennia of evolution, often leans on mathematical patterns to guide structure and function.
Calculating the Fibonacci Sequence
The Fibonacci sequence can be calculated mathematically in two ways.
Regular Method
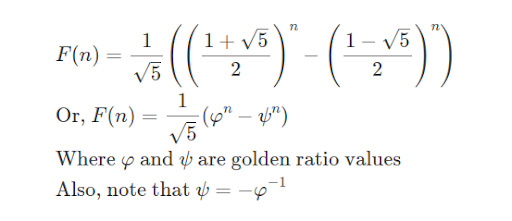
In this approach, each number in the sequence is considered a term, which is represented by the expression Fn.
The n reflects the number’s position in the sequence, starting with zero. For example, the sixth term is referred to as F5, and the seventh term is referred to as F6.
Using this numbering, the Fibonacci sequence can be defined by the following three equations:
- F0 = 0 (applies only to the first integer)
- F1 = 1 (applies only to the second integer)
- Fn = Fn-1 + Fn-2 (applies to all other integers)
The first two equations essentially state that the term in the first position equals 0 and the term in the second position equals 1. The third equation is a recursive formula, which means that each number of the sequence is defined by using the preceding numbers.
For example, to define the fifth number (F4), the terms F2 and F3 must already be defined. These two numbers, in turn, require that the numbers preceding them are already defined. The numbers continuously build on each other throughout the sequence.
Golden Ratio Trick
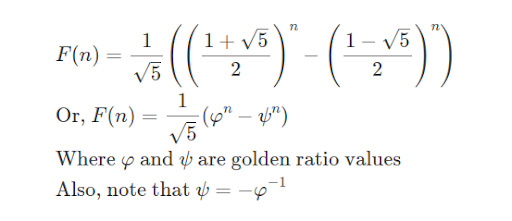
The Fibonacci sequence can be calculated using a mathematical trick involving the golden ratio, which is approximately equal to 1.618. Here’s how it works:
- Start with the first two numbers of the Fibonacci sequence, which are 0 and 1.
- Calculate the next number in the sequence by adding the previous two numbers.
- Repeat this process to generate the entire Fibonacci sequence.
Using the golden ratio trick, you can calculate the nth Fibonacci number (Fn) using the formula:
Fn = (φ^n – (1-φ)^n) / √5
Where φ is the golden ratio (1.618) and √5 is the square root of 5 (approximately 2.236). Here’s an example of calculating the 10th Fibonacci number using this formula:
Fn = (1.618^10 – (1-1.618)^10) / 2.236
Fn = (59.790 – (-0.018)) / 2.236
Fn = 59.808 / 2.236
Fn = 26.776
So, the 10th Fibonacci number is approximately 26.776.
The Appearance of the Fibonacci Sequence in Nature

The Fibonacci sequence, with its simple rule of each number being the sum of the two before it, isn’t just a mathematical curiosity. It weaves its way through the very fabric of the natural world, appearing in a startling array of phenomena. Here are just a few examples:
Plant Growth Patterns
In nature, many plants grow in special patterns. These patterns can be seen in how leaves grow on a stem, how branches spread, and how seeds are placed. One special pattern is called the Fibonacci sequence.
- The Fibonacci sequence is a number pattern that helps plants grow in a smart way. You can see this pattern in sunflowers, trees, and many other plants. It helps plants grow neatly and beautifully.
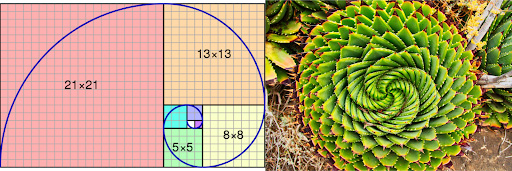
- For example, look at a sunflower. The seeds inside it form spirals. Some spirals turn to the right, and some turn to the left. The number of these spirals follows the Fibonacci pattern. This helps the seeds fit perfectly without crowding.
- Leaves also specially grow around a stem. Each new leaf grows at a small turn from the last one. This helps every leaf get enough sunlight. When leaves get more sunlight, the plant grows better.
- This way of growing is called phyllotaxis, but it simply means “how plant parts are arranged.” It helps plants save space and grow strong.
Even though the Fibonacci sequence is important, it is not the only thing that affects plant growth. Things like plant type, weather, sunlight, and soil also help decide how a plant grows.
Nature uses many smart ideas to help plants grow their best.
Flower Petal Arrangements
Flowers grow their petals smartly and specially. This way is based on a number pattern called the Fibonacci sequence.
- Many flowers have several petals that follow this pattern, like 3, 5, 8, or 13 petals. These numbers help the petals fit nicely together.
- The Fibonacci pattern helps petals grow without crowding each other. This means every petal has enough space to grow strong and healthy.
- Some flowers grow in a spiral shape. These spirals follow the Fibonacci pattern too. The spiral shape helps the flower fit many tiny parts in a small space.
- Because of this pattern, flowers can grow better and spread seeds more easily.
In the end, the Fibonacci pattern helps flowers look beautiful and grow the best way possible. It shows us how nature uses simple math to create amazing designs.
Spiral Shells
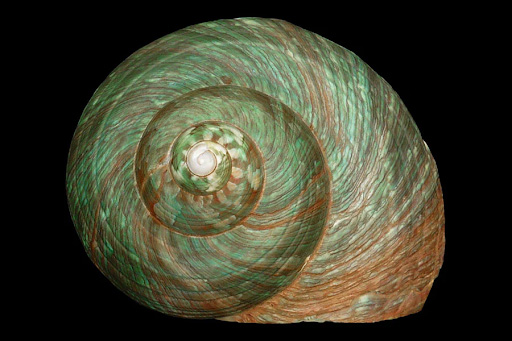
Snail shells and other spiral shells grow in a special curved shape. This shape follows the Fibonacci pattern.
This spiral shape helps the animal in many ways:
- The shell is strong, so it does not break easily.
- The spiral shape uses space wisely as the shell grows.
- Snails carry their shell everywhere, so it needs to be small but strong.
- If you look closely, you can often count spirals on the shell.
- The number of spirals going one way and the other way often matches Fibonacci numbers like 5 and 8.
This shows how nature uses math to build strong and smart designs.
Animal Breeding Patterns
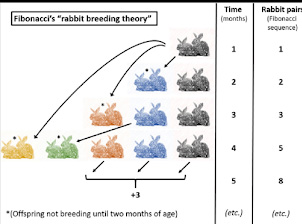
Animals can also follow Fibonacci patterns when they grow in number. A famous example is rabbits.
Here’s how it works:
- Start with one pair of rabbits.
- In the second month, that pair makes one new pair.
- After that, each pair makes a new pair every month.
The number of rabbit pairs becomes:
1, 1, 2, 3, 5, 8, 13…
- At first, the number grows slowly.
- Later, it grows faster as more rabbits can have babies.
This same pattern can happen in other animals like fish, insects, and some mammals.
Mathematical and Evolutionary Explanations
Scientists believe nature uses Fibonacci numbers because they help living things grow better.

Math Helps Nature
- Fibonacci patterns help things fit together neatly.
- Leaves grow in ways that help plants get more sunlight.
- Seeds in sunflowers grow in spirals so they have enough space and food.
Evolutionary Advantages

Evolutionary Advantages:
- Plants and animals that grow in smart patterns can survive better.
- Flowers with certain numbers of petals may attract more bees.
- Strong shells and healthy growth help animals stay safe.
Nature chooses patterns that work best.
The Fibonacci sequence appears to be a fundamental aspect of the natural world, optimizing growth, reproduction, and resource utilization in various organisms.
Conclusion
The Fibonacci sequence appears in nature because it helps plants and animals grow in the smartest and strongest way.
These number patterns help:
- Save space
- Use energy wisely
- Grow strong
- Attract pollinators
From snail shells to flowers to animals, Fibonacci shows us that math and nature work together to make the world beautiful and balanced.
Deepak Wadhwani has over 20 years experience in software/wireless technologies. He has worked with Fortune 500 companies including Intuit, ESRI, Qualcomm, Sprint, Verizon, Vodafone, Nortel, Microsoft and Oracle in over 60 countries. Deepak has worked on Internet marketing projects in San Diego, Los Angeles, Orange Country, Denver, Nashville, Kansas City, New York, San Francisco and Huntsville. Deepak has been a founder of technology Startups for one of the first Cityguides, yellow pages online and web based enterprise solutions. He is an internet marketing and technology expert & co-founder for a San Diego Internet marketing company.



